贝叶斯层级模型（Bayesian Hierarchical Model）是统计分析中一种有效的分析方法，尤其是当变量有很多而且相互之间有说不清道不明的关系的时候
线性回归模型
在介绍贝叶斯分层模型之前，我们先回顾一下线性回归模型。回归分析的目的是估计响应变量y和输入变量X之间的关系。给定一组观察数据${(xi，yi)}_{i=1}^N$，回归模型具有形式： \(\begin{aligned} y_i = f(x_i)+\epsilon_i, i=1,...,n \end{aligned}\)
数据的广泛变化需要适应数据模式的灵活曲线拟合程序。标准参数回归方法（例如多项式回归）使用少量未知参数预先定义函数f。尽管这会产生简约的表示，但最终模型预测精度会比较有限。相反，非参数回归方法对函数f的形式做出了很少的假设，并使用数据驱动的方法来学习F的形状。这会导致灵活的F，可适应所建模的数据类型。一个比较好的方式是分段多项式的非参数回归方法来拟合曲线。
分段贝叶斯回归
令F由几个较低阶多项式函数组成，每个函数在X的不同子空间（局部）上定义，即邻域内的输入点共享相同的功能形式。这些分段多项式函数被连接在一起，以产生光滑的复合函数，并且函数属于连续函数。该定义为：
\[f(x_i)=\sum_{k=1}^{K}\phi_k(x_i)\beta_k\]每一个$\phi_K$表示一个基本函数，$\beta_k$是函数$phi_k$的系数，是一个未知参数。形式化表示如下。
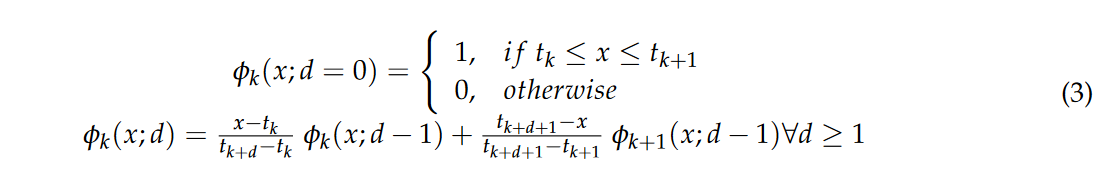
在上面的公式中，有两个重要的参数，分段的数量K， B-样条曲线的次数d。下图展示了不同的分段数量下曲线的差异
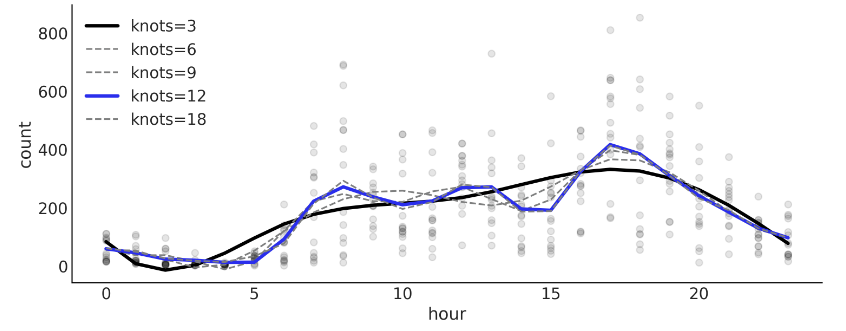0阶时，t处于第i个knot值和第i+1个knot值之间的时候，才会等于1，其他时候都等于0
B-spline函数在不同次数下的表现
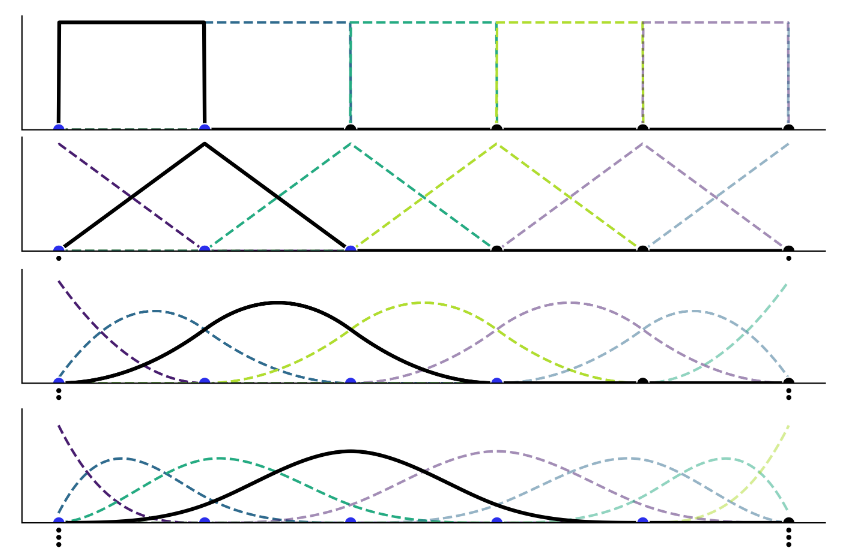
分层建模
在许多情况下，将观察数据视为来自具有相同参数的相同分布是不明智的。以外出就餐为例，学生的用餐偏好可能与老年人的用餐表现不同，因此对学生和老年人的组合使用单一的成功概率是没有意义的。以类似的方式，如果考虑一组网球运动员的发球时间数据，那么使用具有单一均值的单一正态分布来表示这些数据是不合理的 - 平均发球时间快速发球的球员可能会小于慢速球员的平均发球时间。对于许多应用程序，一些观察具有共同的特征，例如年龄或球员，这些特征将它们与其他观察区分开来，因此观察到多个不同的组。
在这里用一个例子来进行说明。考虑一项研究，在该研究中，学生在某一年的 SAT 等标准化考试成绩是从五所不同的高中收集的。假设研究人员有兴趣了解SAT分数与复习时间之间的关系。由于五所不同的学校参与了这项研究，学生的分数可能因学校而异，因此研究人员有必要了解每所学校的平均 SAT 分数并比较学生在学校之间的平均表现。处理这种问题的一种方法是是对每个学校找到单独的估计。对学校j，先找到这个学校的学生$Y_{1j}, Y_{2j},…Y_{nj}$，选择一个先验分布$\phi(\mu_j, \delta_j)$, 并通过贝叶斯推断学习他的均值$\mu_j$和方差$\delta_j$。看上去好像是合理的，但是他忽略了贝叶斯先验分布的均值和方差其实是不独立的。
处理这个问题的另一种方式是忽略分组变量学校，直接假设SAT分数服从具有均值$\mu$， 方差$\delta$正态分布.使用这种方式忽略了学校之间的任何差异，尽管可以合理的假设不同学校的分数是存在一定的相似性，但人有时候这些学校之间并不是无法区分的。
进一步考虑这些学校不仅有中国的学校，还有韩国学校，中国学校的学生与韩国的学校学生的SAT分数有比较大的差异。这时候应该如何做？
一种比较好的方式是使用分层模型，分层模型的使用还减轻了小样本量问题。通过从较高水平借用先验信息，较低水平的样本不足的影响被最小化。利用学生分数之间的潜在层次关系来传递分数曲线之间的知识
考虑L级层次组织，统一层级具有相似的属性。记$i^{th}$下观察数据$x^i$的属性${c_i^1,…c_i^l…c_I^L}$，其中$c_i^l \in \mathbb{Z}^+$表示观察值的级别l的索引。令层级索引的数量$l$为$N^l$，$n^l$表示该组的索引为$l$。例如，我们可能具有三个级别$（L = 3）$，底部级别$（l = 1）$包含来自同一学校，下一个级别$（L = 2）$包含来自统一城市和最高级别$（ l = 3）$包含具有相同国家的数据。值$c_i^{l = 2} = n^{l = 2} = 4$ 表示观察数据i属于城市4。据此，响应$y_i$具有形式： \(\begin{aligned} y_i=\sum_{k=1}^K \phi_k\left(x_i\right) \beta_k^{1, c_i^1}+\epsilon_i \end{aligned}\) 其中K表示基础函数的数量，${\phi_1…\phi_K}$这些基础函数共享所有数据。系数${\beta_1…\beta_K}$在每一层级的每一组都有不同的值。第l层的第$k^{th}$系数的计算如下 \(\begin{aligned} \beta_k^{l, n^l}=\beta_k^{l+1, n^{l+1}}+\xi_k^{l, n^l} \end{aligned}\)
最终用贝叶斯网络图来表示整个模型结构如下所示：
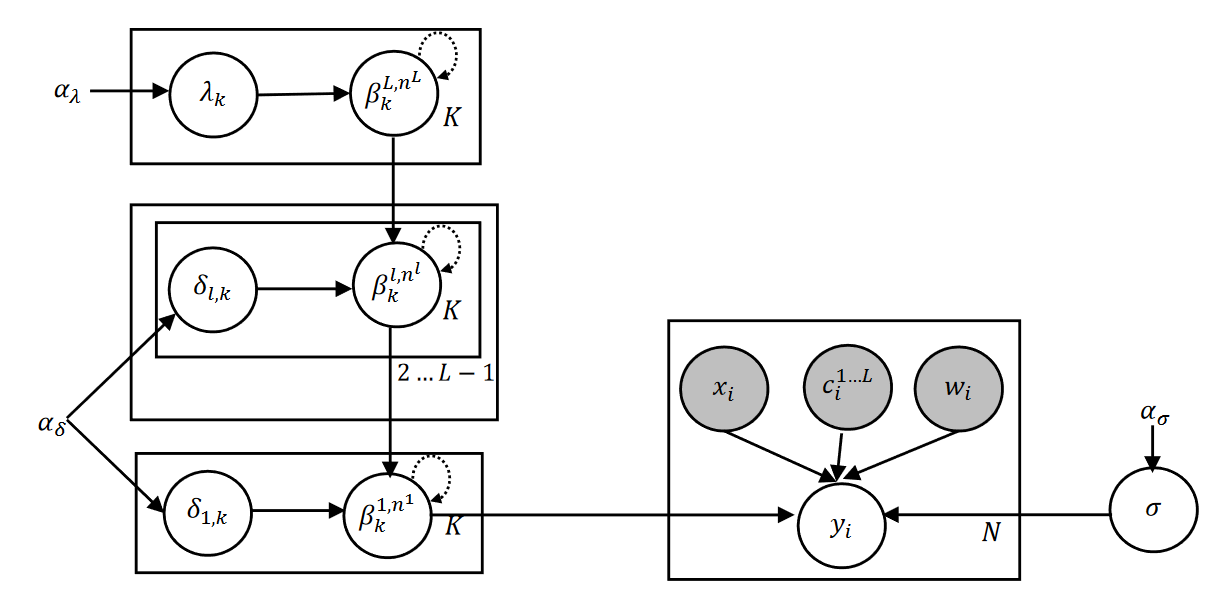
如上图所示，响应结果由回归系数和输入数据来确定，回归系数在各个层级上具有依赖性，在相邻的区间也具有依赖性。 方差变量和超参数在图的右侧显示。
贝叶斯模型需要给定未知参数的先验分布，在观察任何数据之前，先验是我们对参数值的经验认识。在层次模型中，回归系数的先验有几个重要的点：1. 系数的相邻依赖性确保以确保拟合曲线的平滑，顶层系数确定的底层系数的层级依赖性。最终系数的先验：
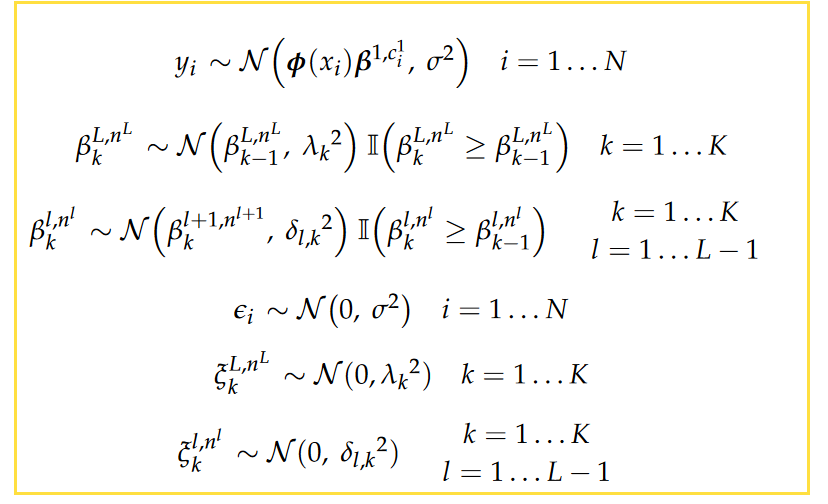
有时候我们需要对样本的观察给与不同的重视程度，在证券交易中，交易规模，交易日期距离是否接近当前。在建模的时候有必要对观测数据进行甲醛，并将样本权重作为回归模型的一部分。
\[\begin{aligned} y_i \sim N\left( \phi(x_i)\beta^{1,c_i^l}, \delta^2/w_i \right) \end{aligned}\]不同的样本具有不一样的方差，这样减少了不重要的样本对模型参数预估的影响
推断过程
贝叶斯模型的核心是依据观察到的数据和参数的先验分布，估算模型参数的后验分布。观察到的数据包括，输入数据， 分层组属性和样本权重。$D = \lbrace x_i, c_i^{1…L}, w_i, y_i\rbrace_{i=1}^N$. 模型参数包括回归系数和方差$\theta = { \beta_{1…K}^{1…L,n^{1…L}}, \sigma, \lambda_{1…K},\delta_{1…L-1, 1…K} }$ 通过前面定义的先验分布。参数的后验分布可以通过如下方程计算
\[\begin{aligned} p(\theta \mid \mathcal{D}) &=\frac{p(\mathcal{D} \mid \theta) p(\theta)}{\int p\left(\mathcal{D} \mid \theta^{\prime}\right) p\left(\theta^{\prime}\right) d \theta^{\prime}} \\ & \propto \prod_{i=1}^N p\left(y_i \mid x_i, c_i^{1 \ldots L}, w_i\right) p\left(\beta_{1 \ldots K}^{1 \ldots L, n^{1 \ldots L}}, \sigma, \lambda_{1 \ldots K}, \delta_{1 \ldots L-1,1 \ldots K}\right) \end{aligned}\]直接计算是比较困难的，必须应用近似推断方法。这也是贝叶斯推断中比较常见的方法，通过MCMC或者是HMC采样的方式来进行参数推断。
