题目: N-BEATS: Neural basis expansion analysis for interpretable time series forecasting
代码: https://link.zhihu.com/?target=https%3A//github.com/amitesh863/nbeats_forecast
Summary
作者提出了一个纯深度学习的模型,用来预测时间序列,在时序竞赛数据上有较好的结果。同时具有一定的可解释性。
Research Objective
- 准确性:较高=> 高(显著、稳定地高于LGB)
- 稳定性:低=> 高(达到统计方法的水准)
- 可调整性: 高(特征、超参、模型结构、训练策略)
- 可解释性:低=> 较高(一定的白盒化能力)
- 执行效率:低=> 高(严格控制模型规模)
Problem Statement
单变量预测,输入的是过去一段时间的数据,预测未来一段时间的数据。虽然作者在文中使用的是单变量预测的结构,但是貌似网上已经有可以增加附加变量的开源实现。
Method(s)
nbeats模型由若干个stack构成,各个stack的结果相加得到最终预测结果;每个stack又有许多block组成,每个block会向前和向后预测,向前预测(Forecast)的结果会加起来计算最终预测结果, 向后预测(Backcast)的结果会和原始信号相减,然后作为下一个block的输入。通过这种方法,可以先预测比较明显的pattern, 之后再预测剩下的部分
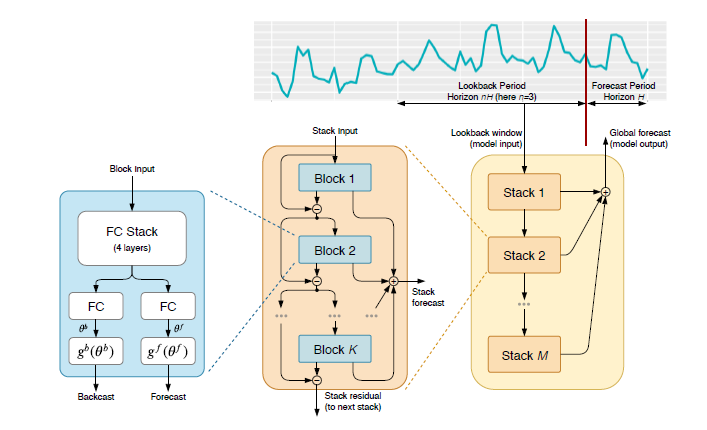
每个block的计算过程:
\[h_{l,1}=FC_{l,1}(x_l)\] \[h_{l,2}=FC_{l,2}(h_{l,1})\] \[h_{l,3}=FC_{l,3}(h_{l,2})\] \[h_{l,4}=FC_{l,4}(h_{l,3})\] \[\theta^b_l=Linear^b_l(h_{l,4})\] \[\theta^f_l=Linear^f_l(h_{l,4})\]接下来,将forecast和backcast预测的结果$\theta$, 结合$g$,即可得到最终结果.
可解释性:
$g^b_l$, $g^f_l$ 即可以是学习出来的参数,也可以是人为设计出的能反映周期或趋势的函数。这样模型的预测就具有一定的可解释性。(这是设计了两个滤波器吗?将符合规律的数据过滤出来???)
论文中作者在stack模块中设计了特定的g函数模拟趋势和季节性分解,以使模型更容易解释
趋势:借鉴统计学模型中通过多项式回归拟合趋势的方法。
\[\widehat{y}_{s,l} = \sum_{i=1}^{p}\theta^{f}_{s,l,i}t_{i}\]其中向量$t$为:$t=[0,1,2,…,H-2,H-1]^T / H$ H是预测窗口的长度.作者构建了随时间缓慢增长的t函数模拟趋势。
周期:周期性的典型特征它是一个有规律的循环反复出现的波动
为了模拟周期性,模型限定 $g^b_{s}l$ 和$g^f_{s}l$ 属于一类周期函数,即:
\[y_t = y_t - \delta\]其中$\delta$ 是周期。在文章中作者使用了周期函数
整个可解释性有两个stack构成:趋势stack,周期性stack
趋势和周期性的预测可作为单独的可解释输出(分别对趋势项stack和周期性stack求和即可)Results
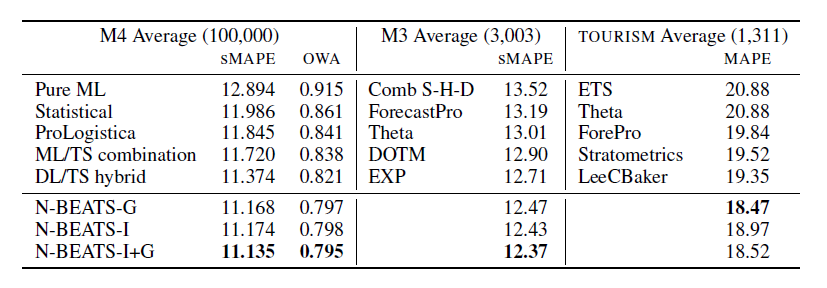
作者基于对比了一系列的模型。基于N-Beats-l+G的效果最好(还是需要ensembling), 作者在Ensemble中对不同的模型使用不同的 loss function、horizon和样本(bagging)
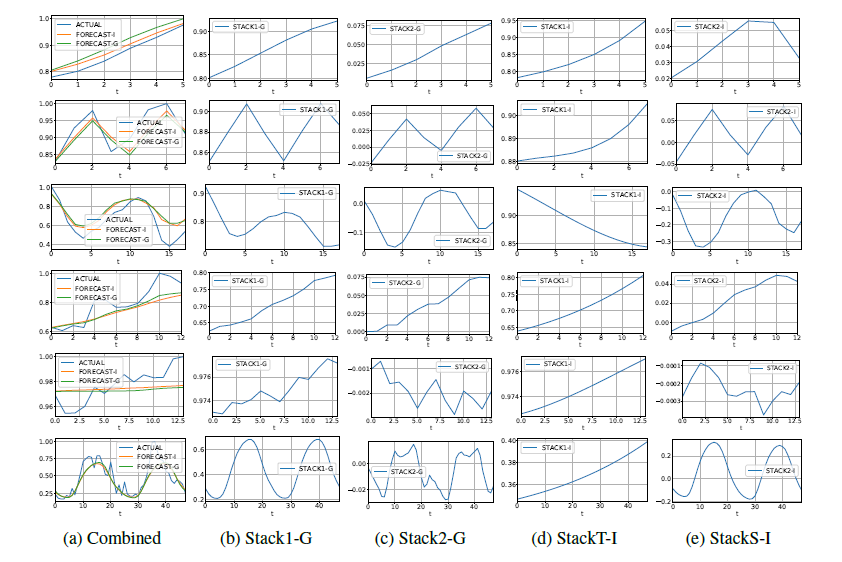
顺便看一下不同stack的对比。标记为G的模型,属于正常的stack, 标记为l的则是指定g函数的stack(模拟周期和趋势)具有一定的解释性. 从下图也可以看出来,N-Beats可以学习出时间序列的趋势和周期。
Evaluation
Conclusion
作者认为:
- 该模型对于单变量的时序预测通用,可解释。
- 模型是一种元学习的形式