EMD

经验模态分解（EMD）介绍

Posted by louis on August 5, 2021

经验模态分解

经验模态分解(Empirical Mode Decomposition, EMD)是依据数据自身的时间尺度特征来进行信号分解，无需预先设定任何基函数，是一种时频域信号处理方式。EMD在处理非平稳及非线性数据上具有明显的优势，适合分析非线性非平稳的信号序列，具有较高的信噪比。

  • 平稳信号：分布参数（均值，方差，协方差等）或者分布规律随着时间不发生变化
  • 非平稳信号：分布参数（均值，方差，协方差等）或者分布规律随着时间发生变化

该方法关键是经验模式分解，使复杂的信号分解为有限个本征模函数(Intrinsic Mode Function, IMF)，分解出来的各个IMF分量包含了原信号的不同时间尺度的局部特征信息。通俗理解就是，EMD是一台机器，将一堆混杂的硬币投进去，其会自动按照1角、5毛、1元等分好

EMD原理

在物理上，如果瞬时频率有意义，那么函数必须是对称的，局部均值为零，并且具有相同的过零点和极值点数目。任何信号都是由若干本征模函数组成，一个本征模函数必须满足以下两个条件：

  1. 函数在整个时间范围内，局部极值点和过零点的数目必须相等或最多相差一个
  2. 在任意时刻点，局部最大值得上包络线和局部最小值的下包络线均值必须为零

对于上述第二条说明：它把经典的全局性要求修改为局部性要求，使瞬时频率不再受不对称波形所形成的不必要的波动所影响, 实际上，这个条件应为“数据的局部均值是零”。但是对于非平稳数据来说，计算局部均值涉及到“局部时间尺度”的概念，而这是很难定义的。因此，在第二个条件中使用了局部极大值包络和局部极小值包络的平均为零来代替，使信号的波形局部对称

EMD将输入信号分解为几个本征模函数和一个残差组成，即由下列公式组成

\[I(n)=\sum_{m=1}^M \operatorname{IMF}_m(n)+\operatorname{Res}_M(n)\]

其中$I(n)$表示输入信号，$\operatorname{IMF}_m(n)$ 表示$M^th$的本征模函数,$\operatorname{Res}_M(n)$表示残差。

EMD分解过程

提取$\operatorname{IMF}$的过程称为筛选，筛选的过程如下:

  1. 标出局部极值点
  2. 通过三次样条插值(cubic spline line)连接极大值点构成上包络线(upper envelope)，连接极小值点构成下包络线(lower envelope)
  3. 求上下包络线的均值$m_1$
  4. 用输入信号减去上下包络线均值
\[X(t)-m_1 = h_1\]

上述过程的一次迭代不能保证$h_1$是本征模函数(IMF)，需要重复上述过程，直到$h_1$是本征模函数(IMF)

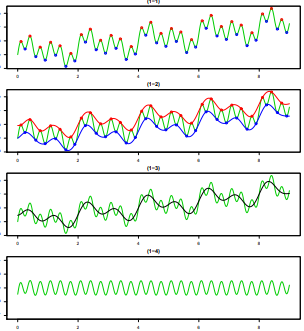
停止准则

停机准则决定了产生一个本征模函数(IMF)筛选过程执行的数目，有如下停机准则

  • 标准偏差(Standard Deviation, SD)
\[SD_k=\sum_{t=0}^{T}\dfrac{|h_{k-1}(t)-h_k(t)|^2}{h_{k-1}^2 (t)}\]

当$\operatorname{SD}$的值小于给定的阈值时，筛选过程停止

  • S Number准则

    定义为过零点和极值点相等或者至多差1的连续筛选数目。一个S-Number被提前设置，只有当S次连续筛选后，每一次过零点和极值点保持相同（相等或者至多差1），筛选过程才停止

  • 阈值方法

    阈值方法设置两个阈值，确保全局小的扰动同时考虑局部大的偏移

选择停机准则后，第一个$\operatorname{IMF}(c_1)$可以获得，$c_1$为包含输入信号最大频率的成分(component)，之后分离$c_1$

\[X(t)-c_1=r_1\]

利用$r_1$作为输入，获得其他的本征模函数

EMD的不足

  • 末端效应

    末端效应发生在信号的开始和结尾，因为在在信号开始之前和结尾之后没有样本点被考虑。大多数情况下，末端点并不是信号的极值，但是在执行EMD的过程中，极值包络线会在末断点发散(diverge)，导致错误，进而扭曲了IMF在末端点的波形，而且这种错误在EMD分解过程中会累积。

  • 模态混叠问题

    模态混叠问题发生在EMD的执行过程中。出现下列情况之一就称为模态混合

    • 在同一个IMF分量中,存在尺度分布范围很宽却又各不相同的信号
    • 在不同的IMF分量中,存在着尺度相近的信号

    模态混叠问题使得特征提取、模型训练、模式识别变得困难，IMF失去了单一特征尺度的特征。集成经验模态分解(Ensemble empirical mode decomposition, EEMD)被提出用来解决模态混叠问题

CATALOG
    CATALOG
      FEATURED TAGS