1. 什么是Holt-Winters
在生活中,常常要根据过去一段时间的数据进行预测,确定业务未来的发展趋势,进而决策,配置相关的营销策略、制定业务目标,由此引申出了一个重要的用数据预测未来的方法——时间序列分析。时间序列预测算法的数据形式以[时间, 观测值]的形式表现。如下图

今天要说到Holt-Winters是利用三次指数平滑来做时间序列预测的方法。Holt-Winters是综合了1957年Holt和1960年Winters两个人的思路的一种方法。在介绍Holt-Winters之前,我们先来了解一下一次指数平滑和二次指数平滑。
一次指数平滑
当时间序列无明显的趋势变化,一次指数平滑表现较好。一次指数平滑的预测公式如下:
\[s_i = \alpha x_i + (1-\alpha )s_{i-1}\]其中 $0<\alpha<1$
$s_i$ 表示第$i$时刻的平滑估计,$s_i$可表示为当前实际值$x_i$和前一时刻的平滑估计值$s_{i-1}$加权求和,权重由$\alpha$决定。将上述公式展开如下:
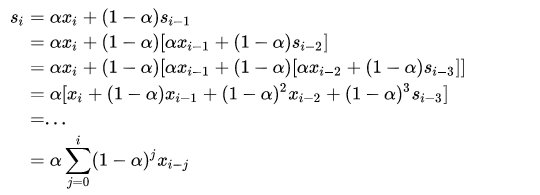
形式和泰勒展开式相似。$\alpha \epsilon [0, 1]$, 越大表示近期的数据影响更大
二次指数平滑
一次指数平滑,没有考虑时间序列的趋势和季节性,二次指数平滑在一次指数平滑的基础上增加了趋势因素。预测公式如下:
\[s_i = \alpha x_i + (1- \alpha )(s_{i-1} + t_{i-1})\] \[t_i = \beta (s_i - s_{i-1}) + (1-\beta )t_{i-1}\]从公式可知,一个时间序列的时刻值分解为baseline部分和趋势部分,t表示趋势,可以表示为连续两个时刻的差值;可知,$t_i$也是一次的指数平滑。
Holt-Winters三次指数平滑
在二次指数平滑基础上,考虑季节性因素,就是三次指数平滑,也就是Holt-Winters。由此,一个时间序列的时刻值分解为baseline部分和趋势部分以及季节部分。由于季节性,存在周期,比如按周,按月等。pi季节性为当前季节性值和上一个周期季节性估计值的加权组合,周期在公式中以k来表示。如下:
\[s_i = \alpha (x_i - p_i) + (1-a)(s_{i-1} + t_{i-1})\] \[t_i = \beta(s_i - s_{i-1}) + (1-\beta)t_{i-1}\] \[p_i = \gamma(x_i - s_i) + (1-\gamma)p_{i-k}\]Holt-Winters 实现
从上面可以知道,要实现Holt-Winters,必须确定:
1
2
3
1. 初始值:s0,t0和p0
2. 合适的参数:alpha,beta, gamma
3. 套入公式即可完成预测
三个重要参数:alpha,beta, gamma都属于[0, 1]之间,要么人为的搜索,要么通过数据来估计,通常采用L-BFGS优化算法来拟合数据。优化算法来自包scipy.optimize的fmin_l_bfgs_b。
下面通过statsmodels包提供的ExponentialSmoothing 来实现holt-winters方法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
from statsmodels.tsa.holtwinters import ExponentialSmoothing
class HoltWintersModel():
def __init__(self, data: TimeSeriesData, params: HoltWintersParams) -> None:
super().__init__(data, params)
if not isinstance(self.data.value, pd.Series):
msg = "Only support univariate time series, but get {type}.".format(
type=type(self.data.value)
)
logging.error(msg)
raise ValueError(msg)
def fit(self, **kwargs) -> None:
"""Fit the model with the specified input parameters
"""
logging.debug("Call fit() with parameters:{kwargs}".format(kwargs=kwargs))
holtwinters = HoltWinters(
self.data.value,
trend=self.params.trend,
damped=self.params.damped,
seasonal=self.params.seasonal,
seasonal_periods=self.params.seasonal_periods,
)
# pyre-fixme[16]: `HoltWintersModel` has no attribute `model`.
self.model = holtwinters.fit()
logging.info("Fitted HoltWinters.")
# pyre-fixme[14]: `predict` overrides method defined in `Model` inconsistently.
def predict(self, steps: int, include_history: bool = False, **kwargs) -> pd.DataFrame:
logging.debug(
"Call predict() with parameters. "
"steps:{steps}, kwargs:{kwargs}".format(steps=steps, kwargs=kwargs)
)
if "freq" not in kwargs:
# pyre-fixme[16]: `HoltWintersModel` has no attribute `freq`.
# pyre-fixme[16]: `HoltWintersModel` has no attribute `data`.
self.freq = pd.infer_freq(self.data.time)
else:
self.freq = kwargs["freq"]
last_date = self.data.time.max()
dates = pd.date_range(start=last_date, periods=steps + 1, freq=self.freq)
# pyre-fixme[16]: `HoltWintersModel` has no attribute `dates`.
self.dates = dates[dates != last_date] # Return correct number of periods
# pyre-fixme[16]: `HoltWintersModel` has no attribute `include_history`.
self.include_history = include_history
if "alpha" in kwargs:
# pyre-fixme[16]: `HoltWintersModel` has no attribute `alpha`.
self.alpha = kwargs["alpha"]
# build empirical CI
error_methods = kwargs.get("error_methods", ["mape"])
train_percentage = kwargs.get("train_percentage", 70)
test_percentage = kwargs.get("test_percentage", 10)
sliding_steps = kwargs.get("sliding_steps", len(self.data) // 5)
multi = kwargs.get("multi", True)
eci = EmpConfidenceInt(
error_methods=error_methods,
data=self.data,
params=self.params,
train_percentage=train_percentage,
test_percentage=test_percentage,
sliding_steps=sliding_steps,
model_class=HoltWintersModel,
confidence_level=1 - self.alpha,
multi=False,
)
logging.debug(
f"""Use EmpConfidenceInt for CI with parameters: error_methods = {error_methods}, train_percentage = {train_percentage},
test_percentage = {test_percentage}, sliding_steps = {sliding_steps}, confidence_level = {1-self.alpha}, multi={multi}."""
)
fcst = eci.get_eci(steps=steps)
# pyre-fixme[16]: `HoltWintersModel` has no attribute `y_fcst`.
self.y_fcst = fcst["fcst"]
else:
# pyre-fixme[16]: `HoltWintersModel` has no attribute `model`.
fcst = self.model.forecast(steps)
self.y_fcst = fcst
fcst = pd.DataFrame({"time": self.dates, "fcst": fcst})
logging.info("Generated forecast data from Holt-Winters model.")
logging.debug("Forecast data: {fcst}".format(fcst=fcst))
if include_history:
history_fcst = self.model.predict(start=0, end=len(self.data.time))
# pyre-fixme[16]: `HoltWintersModel` has no attribute `fcst_df`.
self.fcst_df = pd.concat(
[
pd.DataFrame(
{
"time": self.data.time,
"fcst": history_fcst,
}
),
fcst,
]
)
else:
self.fcst_df = fcst
logging.debug("Return forecast data: {fcst_df}".format(fcst_df=self.fcst_df))
return self.fcst_df
def plot(self):
"""Plot forecast results from the HoltWinters model
"""
logging.info("Generating chart for forecast result from arima model.")
m.Model.plot(self.data, self.fcst_df, include_history=self.include_history)
def __str__(self):
return "HoltWinters"
@staticmethod
def get_parameter_search_space() -> List[Dict[str, Any]]:
"""Get default HoltWinters parameter search space.
Args:
None
Returns:
A dictionary with the default HoltWinters parameter search space
"""
return get_default_holtwinters_parameter_search_space()
从上面实现可知,holt-winters通过预估alpha,beta和gamma来预测。算法的关键就是这三个参数和初始化值。三个参数可以通过优化算法来预估。
总结
本文介绍了时间序列预测算法Holt-Winters以及重要参数的选择的过程。总结如下:
-
Holt-Winters是三次指数平滑,分别为baseline,趋势和季节性;
-
alpha、beta和gamma分别为baseline,趋势和季节性的指数加权参数,一般通过优化算法L-BFGS估计
-
初始化可通过平均值,也可通过时间序列分解得到
-
周期m或者k的选择要根据实际数据来选择
-
Holt-Winters针对波形比较稳定,没有突刺的情况下,效果会比较好